您好,欢迎来到重庆昂扬速才高考培训学校官网!
四、解答题:本题共 5 小题,共 77 分. 解答应写出文字说明、证明过程或演算步骤.
15. 记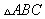 的内角A,B,C的对边分别为a,b,c,已知
的内角A,B,C的对边分别为a,b,c,已知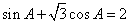 .
.
(1)求A.
(2)若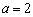 ,
,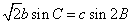 ,求
,求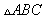 的周长.
的周长.
16. 已知函数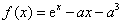 .
.
(1)当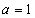 时,求曲线
时,求曲线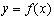 在点
在点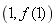 处的切线方程;
处的切线方程;
(2)若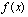 有极小值,且极小值小于0,求a的取值范围.
有极小值,且极小值小于0,求a的取值范围.
17. 如图,平面四边形ABCD中,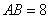 ,
,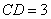 ,
,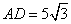 ,
,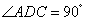 ,
,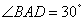 ,点E,
,点E,
F满足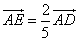 ,
,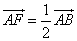 ,将
,将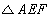 沿EF对折至
沿EF对折至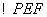 ,使得
,使得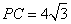 .
.
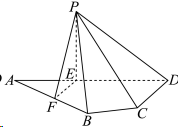
(1)证明: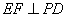 ;
;
(2)求面PCD与面PBF所成的二面角的正弦值.
18. 某投篮比赛分为两个阶段,每个参赛队由两名队员组成,比赛具体规则如下:第一阶段由参赛队中一名队员投篮3次,若3次都未投中,则该队被淘汰,比赛成员为0分;若至少投中一次,则该队进入第二阶段,由该队的另一名队员投篮3次,每次投中得5分,未投中得0分.该队的比赛成绩为第二阶段的得分总和.某参赛队由甲、乙两名队员组成,设甲每次投中的概率为p,乙每次投中的概率为q,各次投中与否相互独立.
(1)若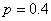 ,
,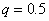 ,甲参加第一阶段比赛,求甲、乙所在队
,甲参加第一阶段比赛,求甲、乙所在队![]() 比赛成绩不少于5分的概率.
比赛成绩不少于5分的概率.
(2)假设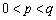 ,
,
(i)为使得甲、乙所在队![]() 比赛成绩为15分的概率最大,应该由谁参加第一阶段比赛?
比赛成绩为15分的概率最大,应该由谁参加第一阶段比赛?
(ii)为使得甲、乙,所在队的比赛成绩的数学期望最大,应该由谁参加第一阶段比赛?
19. 已知双曲线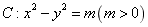 ,点
,点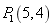 在C上,K为常数,C<K<1.按照如下方式依次构造点
在C上,K为常数,C<K<1.按照如下方式依次构造点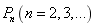 ,过
,过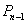 作斜率为 K直线与 C 的左支交于点
作斜率为 K直线与 C 的左支交于点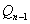 ,令
,令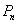 为
为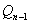 关于Y轴的对称点,记
关于Y轴的对称点,记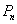 的坐标为
的坐标为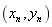 .
.
(1)若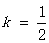 ,求
,求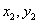 ;
;
(2)证明:数列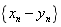 是公比为
是公比为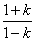 的等比数列;
的等比数列;
(3)设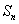 为
为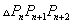
![]() 面积,证明:对任意的正整数 N,
面积,证明:对任意的正整数 N,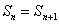 .
.

备注:该2024年重庆新高考Ⅱ数学真题卷【共4页】,第4页;第四大提:解答题;如果有需求领取真题电子版试卷+答案解析;欢迎联系重庆高三艺考生文化课集训班老师添加微信领取,直接电话:185-8116-9688 (微信同号)

添加微信老师,一对一实时问答咨询

加微信,领取近5年新高考真题+答案
联系人:夏老师
电 话: 023-81620016
手 机:185-8116-9688(微信同号)
地 址:重庆市(沙坪坝区,九龙坡区,渝中区,江北区,渝北区,南岸区,巴南区,大渡口区,江津区,北部区);

扫一扫,关注我们

扫一扫,咨询我们
Copyright 2022-2028 重庆昂扬速才高考培训学校官网 https://www.schvip.com All Rights Reserved.
版权所有:高考补习班,高三补习班,艺考文化课培训学校,高三封闭式冲刺班,文化课培训学校,高考文化课集训班,艺考生文化课培训机构,高三辅导班;渝ICP备2025051228号